Assignment: Using the random walker as a model, develop a program that experiments with motion.
Code Example from Pic 1: Gaussian Distribution
Code Example from Pic 2: Gaussian Walker
Process:
I set out this week to explore probability distributions in the context of random walkers. My hope was to create a visualization that allowed participants (not saying users!) to select between a number of real life scenarios that followed common probability distributions (normal, binomial, logarithmic, etc); those probability distributions would inform the behavior of the walker.
Alas, the first week of school and the crazy waitinglist game (and the homework that comes with being in so many classes at once) derailed my ambition. Instead, I learned about how to implement the randomGaussian() function and watched videos about custom probability distributions.
I began by trying to drawing a normal distribution. I managed to get something working here. This isn’t quite a histogram; instead I tied the y position of the ellipse to the conditional statement related to each band of the probability distribution. As a result, this drawing will keep going beyond the canvas, and as a result, after a while the proportions between each band of the distribution become unclear. It’s not the most accurate/efficient implementation, but it confirmed that I was using the Gaussian function correctly.
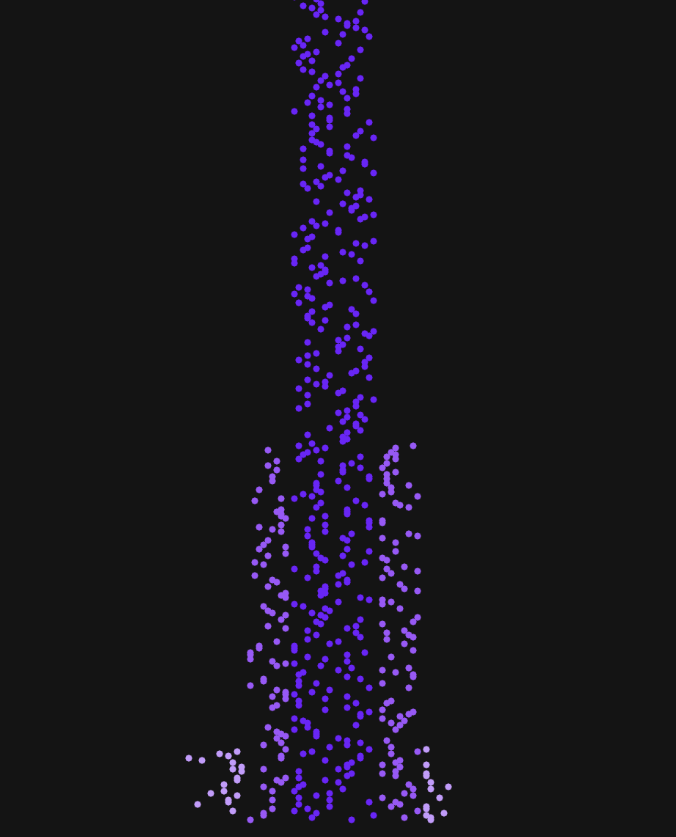
Next, I brought the randomGaussian() function back into the random walker example to inform the step behavior of the walker. Initially, I gave each band of the distribution a different color and different sized step, which made a marginally more interesting version of the Levy flight example presented in course materials. I played with different parameters — fill, colors, magnitude of steps— before landing on one that added something that caught my eye. I tried flipping the pos.x and pos.y variables. I now had an ellipse being drawn at (pos.x,pos.y) at the beginning of each loop and having another drawn at (pos.y,pos.x) when a condition was met. The result was an interesting mirror-image quality to the sketch. In the screenshot below, the image looks a bit like a dancing woman. In other iterations, it’s created something akin to a brain scan. All of them make me think of anti-matter being created in the universe…
Next week I would like to get started on the assignment earlier. I think the best work at the early stages of learning something new comes from making mistakes, interrogating them, adjusting, getting lucky, understanding why, then moving forward with more intention and repeating the cycle. That takes time, and there is a hard limit to the amount of creativity I can imbue into my projects if I only have a day or two!